|
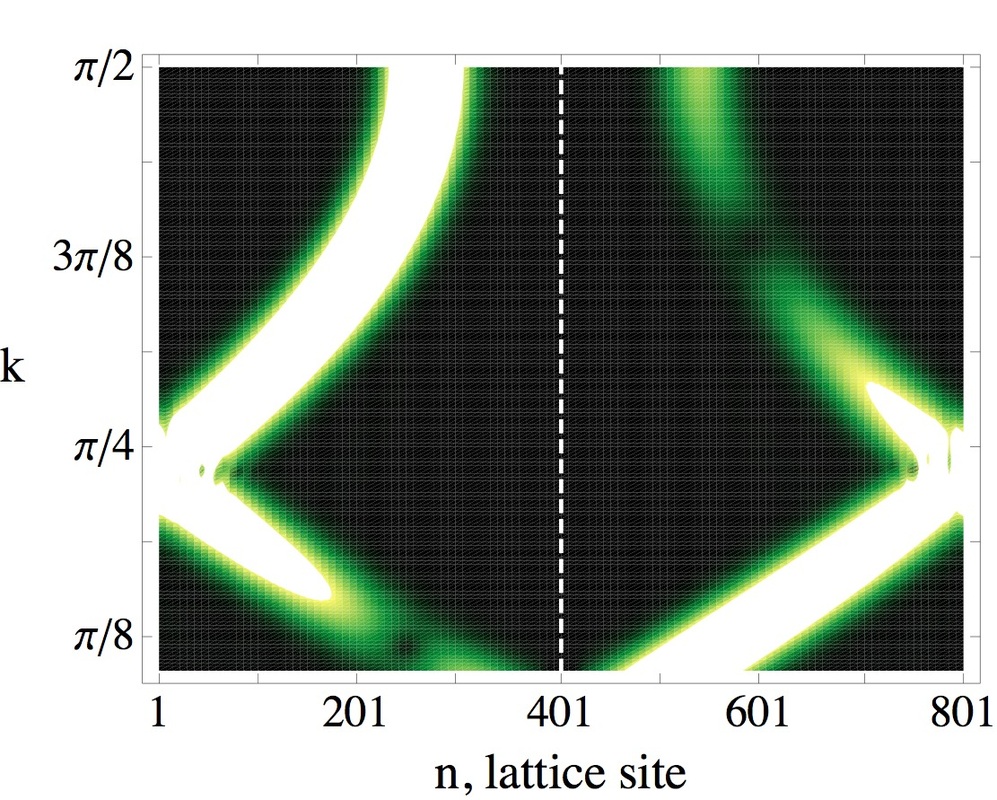
When one or few impurities are placed in an otherwise perfect periodic potential, the translational invariance is broken and the possibility of Fano resonances emerges. These sharp anti-symmetric resonances are characterized by the total reflection of plane waves with determined wave vectors in the impurity region. They occur, when the discrete impurity state is in resonance with the (continuous) band spectrum. Interaction of plane waves with discrete defect modes are ubiquitous, but scattering is not restricted to be caused by linear impurities, it is also observed in nonlinear waveguide arrays: Nonlinearity can generate several scattering channels leading to resonances due to destructive interference and, as a consequence, to total absence of transmission similar to the original Fano problem.
|
Adding not only a few impurities, but disorder to the whole periodic system leads to the destruction of periodicity, the breaking up of the band structure and to the onset
of a complete localization of the eigenmodes in 1D and 2D non-correlated lattices. The smallest amount of disorder causes exponentially localized Anderson modes and the absence of wave propagation. But, within the localization volume,the presence of weak disorder promotes a more uniform spreading and distribution of a wave packet; an effect that is further enhanced by the presence of a focusing nonlinearity. For short-range correlated binary arrays, the existence of extended states may lead to long-range transport and anomalous wavepacket evolution. If disorder is absent in the bulk of the system, but affects the boundary of the array, an asymptotic packet localization in the center of the array can be observed.
of a complete localization of the eigenmodes in 1D and 2D non-correlated lattices. The smallest amount of disorder causes exponentially localized Anderson modes and the absence of wave propagation. But, within the localization volume,the presence of weak disorder promotes a more uniform spreading and distribution of a wave packet; an effect that is further enhanced by the presence of a focusing nonlinearity. For short-range correlated binary arrays, the existence of extended states may lead to long-range transport and anomalous wavepacket evolution. If disorder is absent in the bulk of the system, but affects the boundary of the array, an asymptotic packet localization in the center of the array can be observed.
|
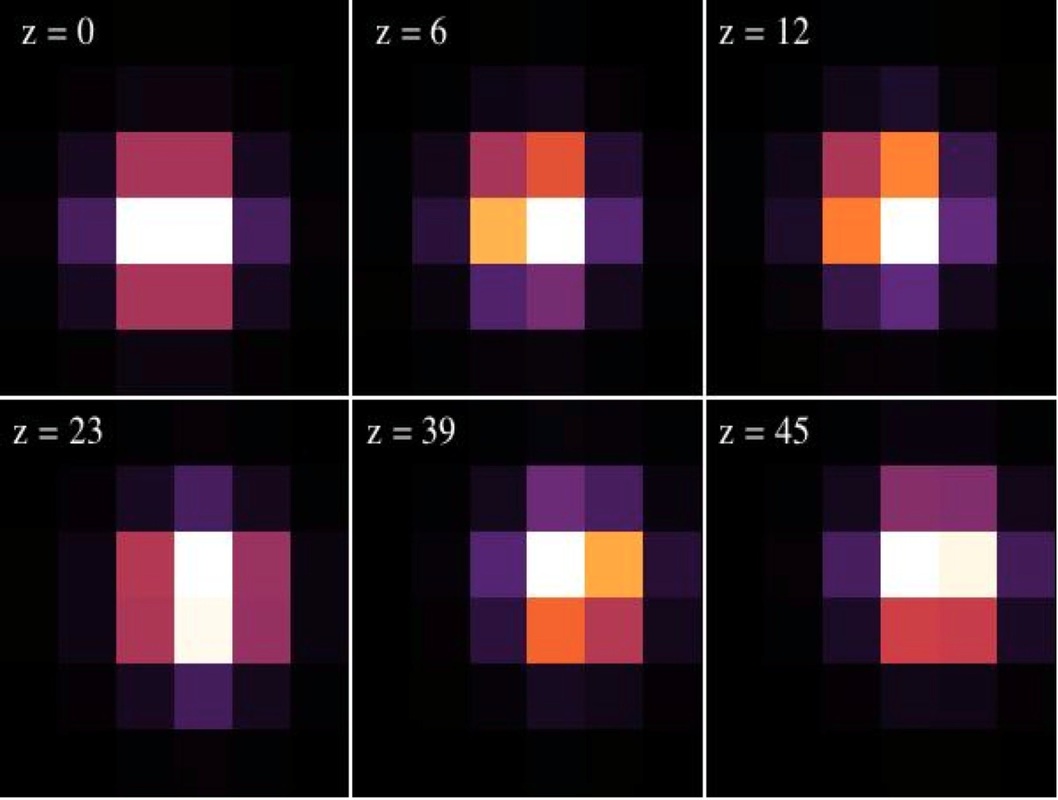
Localized modes are not only caused by defects or disorder - discrete nonlinear systems may support self-localized modes in balance between discrete diffraction and the nonlinearity of the medium. The critical nonlinearity value necessary to dynamically localize energy in discrete nonlinear lattices can be found focusing on the effective frequency and participation ratio of the profile, it defines the transition in parameter space from a delocalized to a localized profile in ordered, disordered and quantum Glauber-Fock lattices. In contrast to the soliton solutions of the continuous and homogeneous nonlinear Schrödinger equation, which are mobile by definition, nonlinear localized stationary modes of discrete Schrödinger lattices are in general immobile. Discreteness and nonlinearity impose an energy barrier - the Peierls-Nabarro potential - that any mode has to overcome in order to move from one lattice site to the next. For certain nonlinearity classes, there are regions of stability exchange between the fundamental modes, associated with the appearance of intermediate, asymmetric modes, causing an effective energy barrier.
|
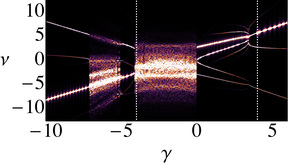
When the coupling between nonlinear quantum oscillators is sufficiently strong, the Rotating wave approximation does not hold any more and an approach beyond perturbation theory is necessary. Quantum fluctuations provoke the loss of the symmetry related to the particle number conservation and cause the system to become non-integrable within the meanfield description. The emerging chaotic regimes can be clearly identified in the meanfield-limit and are also present in the full quantum model. These phenomena are also present in an extended chain of ultra-strongly coupled oscillators.
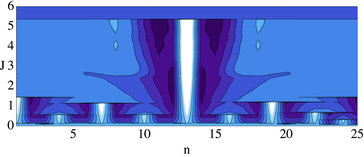
Considering open Bose-Hubbard chains beyond the meanfield approximation any localized state is predetermined to decay. An additional, carefully designed, gain may be able to recover stationary and dynamically stable localized states as well as a localized oscillating solution type. As an anti-continuous limit is forbidden for quantum lattices, the appearance of localized modes has to happen differently. We find a train of symmetry-breaking bifurcations connecting the homogeneous phases to new ripple phases with changing periodicity, to static and periodic stable localized modes and back to a homogeneous solution.